Calculating the Required Energy of Drilling into Europa

Drilling into Europa would be a huge engineering challenge. To demonstrate, I’ll calculate the required energy to pierce Europa’s ice surface.

Picture this: Europa, one of Jupiter’s moons, is a whopping 390 million miles from Earth. It’s tinier than our own moon, but get this – it’s thought to have double the water of all Earth’s oceans combined! The catch? It’s all hidden beneath a massive ice sheet.

Our calculations may be pure sci-fi for now, but who knows? They could turn into reality someday…

Why are we looking for life on Europa?

Simple: we want to know we’re not alone.

Europa’s got a vibe pretty similar to Earth, which means there could be a perfect cocktail of chemicals for life brewing in its oceans. Here’s a quick comparison between Earth and Europa:

Comparison metrics	Earth	Europa
Average ocean depth	2.3 miles	62.1 miles
Volume of water	0.31 billion cubic miles	0.65 billion to 0.96 billion cubic miles
Diameter	7,917.5 miles	1,900 miles
Average distance from Sun	93 million miles	485 million miles
Surface gravity	7.46 times that of Europa	0.13 times that of Earth
Surface pressure	1 bar	10^(-12) bar

But don’t kid yourself – a trip to Europa would be anything but easy. It’s such a hostile place that it makes Mars look like a sweet getaway.

With today’s tech, humans wouldn’t stand a chance. But robots? They might just pull it off later this century.

Europa’s icy armor

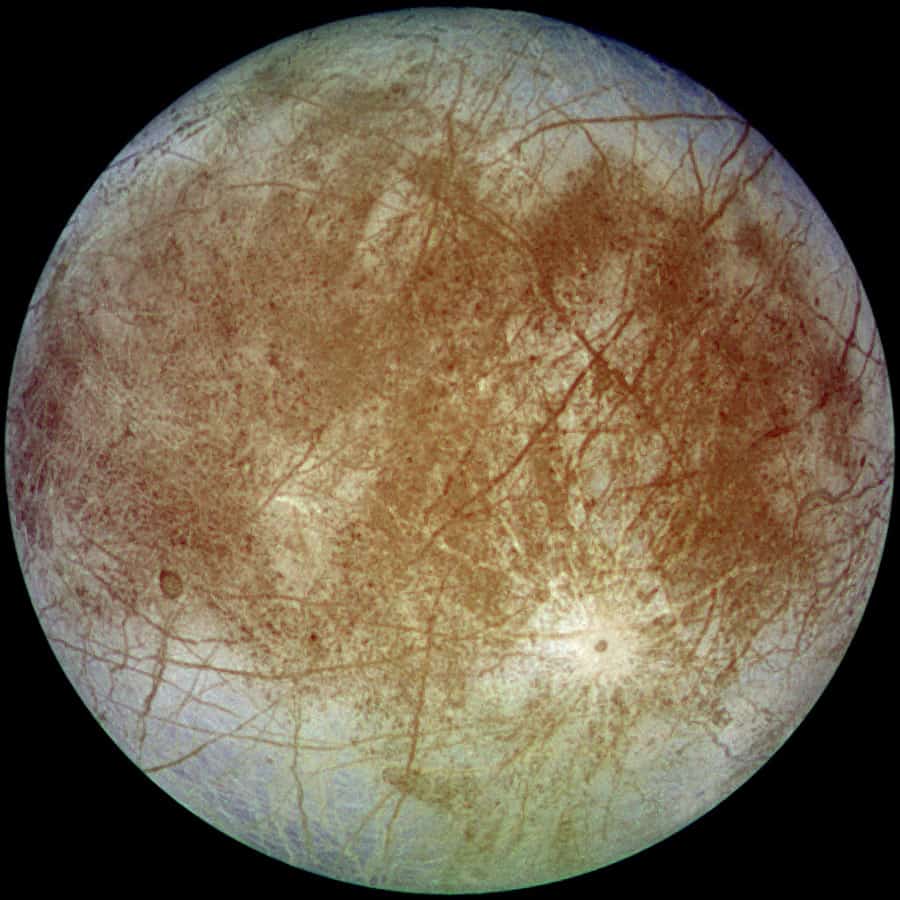
NASA tells us that Europa’s icy shell averages about 25 kilometers thick, concealing an ocean 60 to 150 kilometers deep. Picture Antarctica, but crank up the hostility by 1000x!

For our calculations, let’s say we need to break through 25 kilometers of ice.

The perfect manmade hole in Europa’s ice sheet

There are two following schools of thought on the hole size:

1. Go big
2. Keep it small

Simple enough, right? Let’s weigh our options.

Drill a big hole: This would give us a large, permanent access point, perfect for all sorts of ocean research – maybe even a mini-submarine!

The downside? It’s pricey and tough to pull off. Jupiter’s tidal forces could cause the ice to shift non-stop, which might make this option a no-go. Plus, bigger holes take longer to drill, and that means more things could go wrong.

Melt a small hole: A Cryobot, a nifty robot that melts through ice using heat, could do the trick. These robots typically weigh 25 kilograms and measure 1 meter in length with a 0.06-meter radius. So, we’d just need a hole big enough for one of them.

The ideal hole size: The small one’s a no-brainer. Honestly, we might only need to drill down 100 meters. Then, we can send the analyzed ice sample data back to Earth.

To make our calculation interesting, let’s settle on a 1-meter hole diameter.

Discovering the perfect spot to break through Europa’s ice sheet

To find the best entry point, we need to keep a few things in mind:

• Steer clear of fault zones, so we don’t accidentally set off massive ice movements.
• Aim for thin ice regions, making drilling easier.
• Dodge huge cracks that could cause trouble for our tunneling efforts.
• Avoid areas where Jupiter’s tidal forces are greatest.

Europa’s icy secrets: How to reach its mysterious ocean

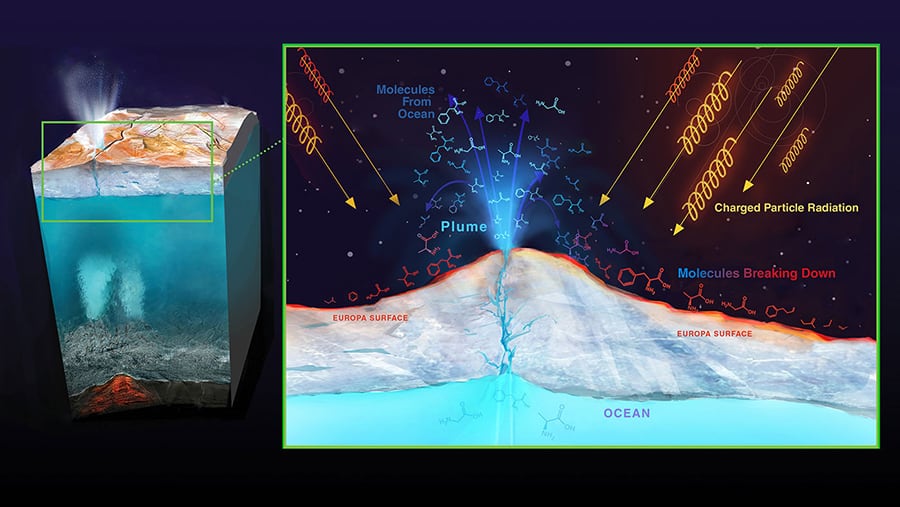
Get ready for a thrilling adventure as we explore three innovative techniques to unlock the hidden ocean beneath Europa’s icy surface:

1. Drilling into the ice sheet
2. Melting through the ice sheet
3. Melting through the ice sheet with a lid covering the hole opening

Method #1: Drilling into the ice sheet

Step #1: We’ll start by calculating the mass of the ice column we need to remove. Picture a 1-meter wide, 25-kilometer long ice column.

Where,

= ice column mass
= ice density is
= ice column height
= hole radius

Step #2: Now, let’s figure out the potential energy needed to lift all that ice out of the hole. We’ll assume the ice column removal will be at a constant speed. This way, work isn’t turned into kinetic energy.

Where,

= potential energy
= ice column mass
= Europa’s gravitational force is 1.315 m/s²
= ice column height

We need a 164.4-megawatt electric generator, to produce electricity for 1 hour. Then assuming a generator efficiency of 50%, the figure doubles to 328.8MWh!

Now, the whole electrical infrastructure needed to back this generator is a totally different beast. But just for kicks, you might want to take a look at my article about drilling into Mars with a mega drill. On Europa, we wouldn’t need such a gigantic drill, but we’d still have to bring along a pretty hefty drill and millions of tons of shoring equipment.

Method #2: Melting through the ice sheet 

Imagine a nuclear-powered drilling bot melting the ice as it descends deeper and deeper. This method is pretty neat since it doesn’t need a lot of heavy equipment and there are fewer moving parts, leading to more reliability!

Step #1: Calculate the energy to raise the temperature of the ice column from -160°C to -75°C.

At −75 °C and under near-vacuum conditions of 10⁻⁶ bar, ice sublimation should occur in theory. Europa has a surface pressure of 10⁻¹² bar, and a surface temperature of -160°C.

The energy required to heat the ice column is

Where,

= energy required to increase the temperature
= ice column mass
= specific heat of ice is 2,108 joules/kg°C
= change of temperature

Step #2: Calculate the energy for the enthalpy of fusion of ice and the enthalpy of vaporization.

We need to figure out how much energy is needed to change the state of a substance without raising its temperature. In this case, we’re going from ice to vapor.

The enthalpy of fusion of ice is 333,550 joules/kg to transform ice to liquid.

The enthalpy of vaporization of water is 2,257,000 joules/kg to go from liquid to steam.

Step #3: Calculate the total energy required.

Method #3: Melting through the ice sheet with a lid covering the opening

Step #1: We place a lid on top of the hole and pressurize it to about 1 atmosphere (the same air pressure we have on Earth at sea level).

Doing this will keep the melted ice liquid, meaning we don’t need extra energy to boil the water away like we calculated in Method #2.

Plus, the weight of the water should create enough pressure to prevent the tunnel from collapsing inwards, so we won’t need a 25-kilometer tunnel wall.

Step #2: By consulting the phase diagram of water, we can find the new phase change temperature at 1 atmosphere. We’ll need to increase the ice temperature from a bone-chilling -160°C to a manageable 0°C to liquefy that ice.

Step #3: Calculate the energy for enthalpy of fusion of ice.

Step #4: Calculate the total energy required.

The selection for the best method to penetrate Europa’s ice

I’m all in for Method #3, even though Method #1 would need less energy. Trust me, as someone who’s been around mega drills, Method #1 just doesn’t seem practical. There are too many potential hiccups, and with no humans on this mission, we’d better not lug unnecessary equipment across the 390-million-mile journey to Europa.

Calculation assumptions

Keep in mind that these 3 techniques are just ideas, which have been debated for decades. My calculations are admittedly oversimplified and far from perfect, considering the mission’s complexity and many unknowns.

For some clarity, here are the 10 basic assumptions I made:

Assumption #1: Insulating the tunnel wall

As we drill into the ice sheet, we’ll need to slide in thick metallic tubing all the way down. We’ll use steel, high in nickel, making it less likely to break in low temperatures.

Without the tubing, the tunnel might just freeze up again behind our machines in Methods #1 and #2. And let’s not forget, the tunnel could also deform from the immense pressures around it. Jupiter’s gravitational forces will flex the ice sheets, causing the tunneling to possibly snap.

Moreover, while the top of the ice sheet is as hard as granite, the deeper you go, the gooier the ice becomes as it transitions to liquid. So, we’d need to switch to a different material at some point.

Assumption #2: Building the tunnel wall quickly

Ice forms when water molecules slow down due to low energy. Add some heat, and they start zipping around.

In Method #2, after melting the ice, we’d face a huge challenge with a tunnel depth of 25 kilometers. The ice might quickly reform as water molecules get further from the heat source.

Lake Vostok is a guiding example from Earth

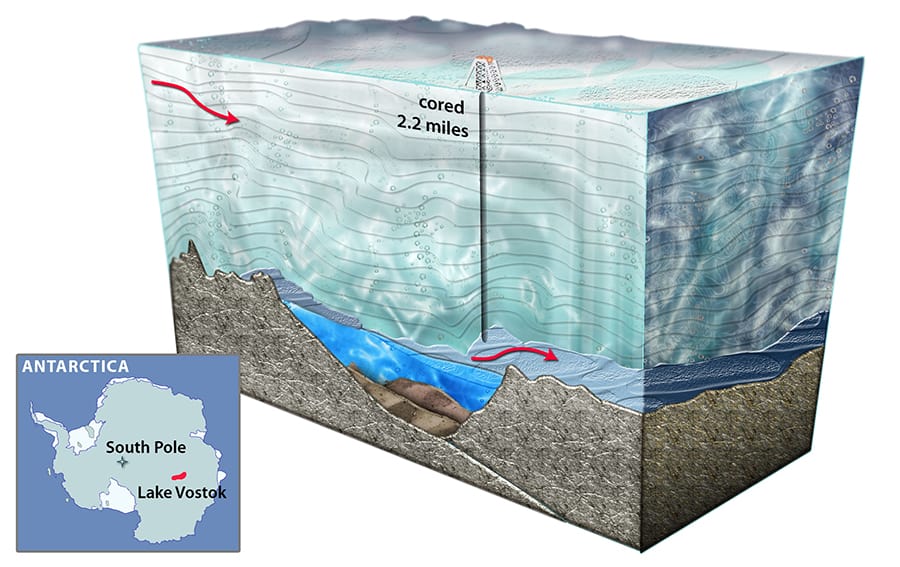
We can look to Earth’s Lake Vostok as a guide. The pressure there is a whopping 350 atm (35 MPA), thanks to our planet’s greater gravity according to Antarctic Ecosystem. This results in a frosty -3°C liquid water temperature beneath the ice.

Undaunted, the Russians drilled 4 kilometers into Lake Vostok without installing steel walls. They melted incoming ice by pouring kerosene and freon down the borehole and then pumped it out.

They carried this out during the warmer months when surface temperatures were a mere -50°C. After all, in the wrong months, it can plummet to -89°C.

On Europa, though, the surface temperature is a bone-chilling -160°C, and the tunneling goes 25 kilometers. But, Europa’s ocean could be warmer than Lake Vostok according to the phase diagram of water, probably due to pressures as high as 130-260 MPa on its ocean floor – way higher than what’s found at Lake Vostok.

Assumption #3: Heat loss to the icy tunnel wall

In Methods #2 and #3, the surrounding tunnel ice will conduct heat away. In return, the energy required to create the tunnel would increase, as machine efficiency drops. I didn’t factor this heat loss into my calculations.

Assumption #4: Ice column is a uniform -160°C

The surface temperature of Europa is -160°C. I assumed the entire ice column has a uniform -160°C temperature.

However, a thermal gradient does exist. The deeper you go, the warmer it gets. If it didn’t, there’d be no liquid ocean beneath the ice, as we’re assuming. Based on the phase diagram of water, the temperature would be 0°C at the bottom of the ice sheet.

Assumption #5: Recondensing of sublimated ice

An insulated barrier would hug the inner tunnel wall in Method #2, as discussed in Assumption #2. This would keep recondensation at bay and prevent our machinery from getting stuck.

Assumption #6: Machine weight

I didn’t consider gravitational acceleration from the machines. Heavier machines exert a greater force on the ice, making the tunneling easier.

In the same vein, if the force of gravity is small, machines will exert less force on the ice. This is because of the reduced contact between the machine and the ice.

Europa has a gravitational force of roughly 1/9 of Earth. So it’s best to use heavy machines.

To illustrate this concept, imagine heating up water. The water molecules will work against the surrounding atmosphere and expand. But on Europa, the expansion requires less work due to the moon’s thin atmosphere or low pressure. There’s nothing for the water molecules to push against.

So, the energy for expansion is negligible for pressures different than 1 atm. Especially, when compared to the high amount of energy needed to heat up water.

I used the specific heat value calculated at 1 atm in Method #3. But we wouldn’t lose much accuracy by using the specific heat value calculated on Earth at sea level.

But, theoretical data mixed with computed data gives us insight. The sublimation of ice is unlikely below -223°C in cosmic conditions, and impossible at -250°C. I used -75°C in Method #2

I assumed from the sublimated ice, a steam jet would remove the tailings without added energy. But, as we learned in Assumption #1, the water vapor may turn back into ice. Given Europa’s thin atmosphere, the other assumption is the ice wouldn’t reform easily.

For Method #1, a solution doesn’t exist to remove the column tailings. These are the broken off ice pieces in the tunnel.

Assumption #10: Pressurizing the tunnel

To pull off Method #3, we need to pressurize the tunnel to 1 atm. This is an engineering feat of its own.

The goal of drilling into Europa

Sure, finding a natural crevice to sneak into would be way easier. Some folks even think Europa has cryovolcanoes. But that wouldn’t be nearly as thrilling as melting and drilling through Europa’s icy surface.

Our mission is to dream up sci-fi engineering on steroids. Because who knows? One day, we might need to put this wild tech into action…

What are your thoughts on drilling into Europa? What other challenges do you foresee? 

---

Featured Image Photo Credit: NASA