A low power factor affects electric utilities differently. I’ll show the impact through a simple utility power factor penalty calculation.
By the end, you’ll see why big utility customers are committed to maintaining a good power factor.
But before we dive into any number crunching, let’s break down the different types of electrical power.
Power factor and types of electrical power
Ever heard of power factor? It’s a simple concept that shows the relationship between real power and apparent power in an electrical circuit. Put simply, it tells you how much actual power a circuit uses compared to what it looks like it’s drawing from the power source.
To put it another way, power factor measures how well a load matches a resistive load. A purely resistive load has a power factor of 1. Other loads, like transformers and induction motors, have a power factor less than 1 and need reactive power to work.
Let’s break down the three types of electrical power to make this crystal clear:
Real power (P)
This is the energy a load entirely consumes and changes into a different form, like heat, light, or mechanical power. We measure real power in watts (W).
Reactive power (Q)
Reactive power deals with electrical energy that’s stored and then released, like in a magnetic or electrostatic field for an inductor or capacitor.
Consider an induction motor. It requires reactive current to create the rotating magnetic field that turns real electrical power into mechanical power. This magnetic field stores energy that moves to and from the power source as the magnetic field polarity flips. Likewise, this energy can also shift to and from power factor compensation capacitors, which helps to stabilize the system’s power factor.
We measure reactive power in volt-amperes reactive (VARs).
Apparent power (S)
This is the total power in an AC circuit, both dissipated and absorbed. It’s a mix of reactive power and real power. We measure apparent power in volt-amperes (VAs).
We measure apparent power in volt-amperes (VAs).
To help you picture how these power relationships work, check out the power factor triangle below. Keep in mind that apparent power is the hypotenuse, and you can use the Pythagorean theorem to calculate it.
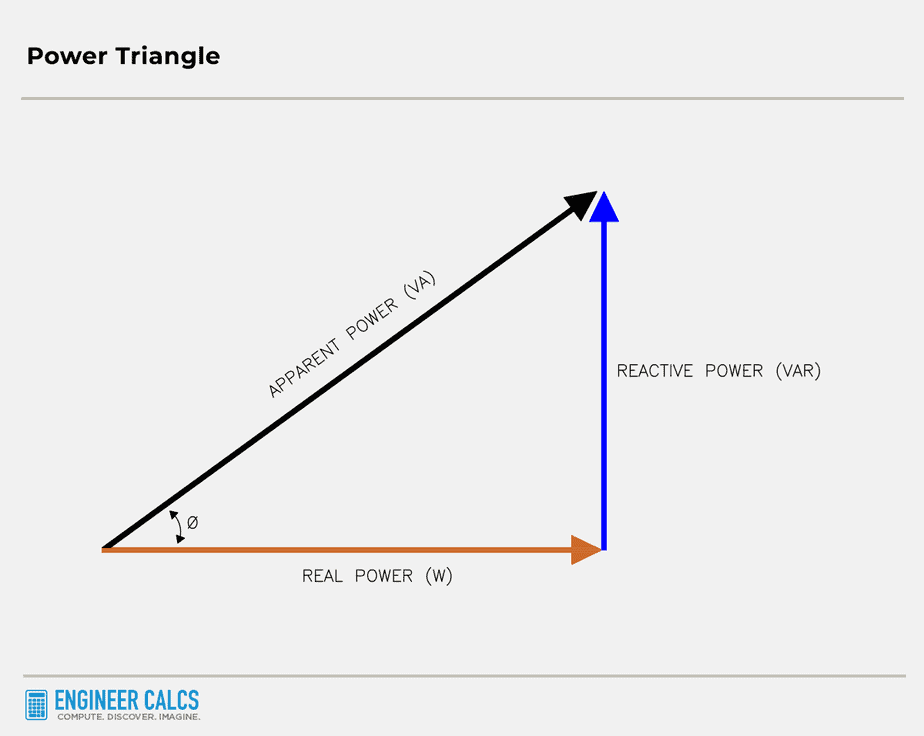
Why does power factor matter to utilities?
Let’s discuss why it’s crucial for utilities to maintain a solid power factor, to the extent that they’ll penalize customers if their power factor falls too low.
Generators
You might have noticed that most generators have a power factor rating of 0.8. That’s because they need to support lagging power factor loads, like the numerous induction motors in water treatment facilities.
Imagine a 100 kVA generator with a power factor of 0.8. The full load kW capacity is 80% of the load kVA, as long as the power factor remains at this level.
P = 80 kW is the maximum power the generator can supply
%
But what if the power factor drops below 0.8? The total kVA increases, reducing the generator’s capacity due to the higher lagging reactive kVA component. This surge in current flow can even cause a voltage drop.
At times, if you retrofit a facility without proper planning, it can lower the power factor. For instance, connecting more induction motors to the generator than it was designed for forces the generator to work harder to support the extra magnetic fields, leading to a reduced power factor.
Important Note: Reactive power isn’t useless. Sure, it doesn’t do real work, but AC machines wouldn’t work without it.
Picture electric motors—they spin and get things done through the interaction of magnetizing fields created in the motor windings. These magnetic fields need a source of magnetism, which comes from the AC line they’re connected to. The catch? The magnetizing kVAR lowers the power factor.
Transformers
Transformers rely on a magnetic field to convert power from a primary to a secondary voltage. Just like generators, a load’s power factor can affect a transformer’s real power capacity.
If a load’s power factor keeps dropping, it demands higher current draw and pushes the transformer past its limits, negatively impacting voltage regulation.
Distribution line losses
When it comes to electric circuits, the wire size used by utilities is crucial for carrying the required current. But what happens when a connected customer’s power factor takes a nosedive?
As the power factor drops, the circuit has to carry a larger reactive kVA component on top of the kW, meaning more current flows through the wires. The result? Utilities need to install bigger wires! But that’s not the only headache. The resistance losses (
) of the conductor can also trigger a voltage drop at the load end of the lines, a common issue with lousy power factor.
Going a bit deeper, the same problem pops up with current limiting reactors. These are just big coils of wire that generate a magnetic field. You can use current-limiting reactors to cut down short-circuit current, but they’ll also lower your power system’s power factor.
Wanna learn more? Check out my article on sizing a current limiting reactor for a substation. It’ll help you better grasp inductive loads and the principles involved.
Power cost
A utility kilowatt-hour (kWh) meter tracks your energy usage. That’s how utilities figure out how much to charge you based on your energy consumption.
But here’s the deal: besides the kWh charge, utilities can also slap penalties on you for having a low power factor in their billing rates. On the flip side, they give incentives for maintaining a high power factor.
Here’s an example. Line losses change based on the square of the line current (). And with a lower power factor, the line current is higher. Naturally, the utility isn’t going to foot the bill for the customer.
Important Note: There are perks to buying power through a power factor clause. The customer benefits when they have a high power factor.
Costs incurred by electric utilities due to poor power factor
Electric utilities have the vital task of supplying power to all their customers, including meeting their reactive power needs. To ensure everyone gets what they need, utilities often have to upgrade their gear, like generators, transformers, power lines, and other electrical stuff. But, of course, this all comes at a price!
To cover these costs, utilities impose a power factor penalty that can make up a big chunk of a customer’s bill. But there’s a silver lining! Customers can install capacitors and save a ton of money, completely eliminating the utility power factor penalty!
Important Note: Adding more inductive loads to a power system leads to an increase in apparent power due to the rise in lagging reactive power.
The formula for apparent power is
Power factor correction capacitors offer a solution to enhance power factor by providing leading reactive power that cancels out the lagging reactive power. In a nutshell, capacitive loads improve the power factor, while inductive loads bring it down.
Utility power factor penalty calculation
Alright, let’s dive into the nitty-gritty of how installing capacitors can save you a pretty penny. To keep things simple, I’ll use standard utility rates you’ll find across most of the U.S.
Demand charge:
| Rates (Demand Charge) | Per Meter, Per Month |
|---|---|
| First 1,000 kW of billing demand | $10,500.00 |
| Over 1,000 kW of billing demand, per kW | $12.00 |
Energy charge:
| Rates (Energy Charge) | Per Meter, Per Month |
|---|---|
| First 100 kWh per kW of billing demand per kWh | $0.22 |
| Next 300 kWh per kW of billing demand per kWh | $0.28 |
| All excess, per kWh | $0.35 |
Important Note: Let’s clarify what Power Factor Charge and Fuel Cost Adjustment mean.
Power Factor Charge: We’ll use the rates listed above for our calculations. The total charge for a given month goes up or down by 0.1% for each 1% that the customer’s average power factor is above or below 85%. We’ll find the average power factor by comparing lagging kilovolt ampere-hours to kilowatt-hours, all based on a month’s data.
Fuel Cost Adjustment: This is figured out by multiplying the total billed kilowatt-hours by $0.006 per kWh. This amount isn’t affected by adjustments for voltage or power factor. The $0.006 adjustment represents the revenue needed to cover power production costs. The utility compares the real cost of fuel and purchased power to the costs they projected since energy costs can change.
EXAMPLE: Picture Factory Z with a 5,000 kW load at a 0.65 power factor. They use 3,750,000 kWh/month of electricity and buy their power from Utility X.
Demand charge
First 1,000 kW = $10,500.00
Over 1,000 kW (bill at $12.00 per kW) = (5,000 kW – 1,000 kW) x $12.00/kW = $48,000.00
Demand charge subtotal: $10,500.00 + $48,000.00 = $58,500.00
Energy charge
First 100 kWh/kW demand (100 x 5,000 x $0.22) = $110,000.00
Next 200 kWh/kW demand (300 x 5,000 x $0.28) = $420,000.00
All excess kWh (3,750,000 – [100 x 5,000] + [300 x 5,000]) x $0.35 = 1,750,000 x $0.35 = $612,500.00
Energy charge subtotal: $110,000.00 + $420,000.00 + $612,500.00 = $1,142,500.00
Now, let’s add the demand and energy subtotals together.
$58,500.00 + $1,142,500.00 = $1,201,000.00
Power factor penalty
(85-65) x 0.001 x $1,201,000.00
20 x 0.001 x $1,201,000.00 = $24,020.00
Fuel cost adjustment
3,750,000 kWh/month x $0.006/kWh = $22,500.00
Total monthly bill
Now, we add all the following charges together:
- Demand charge
- Energy charge
- Power factor penalty
- Fuel cost adjustment
Total: $1,201,000.00 + $24,020.00 + $22,500.00 = $1,247,520.00
Utility power factor calculation with capacitors installed
Let’s dive back into the numbers and see how capacitors can improve our power factor to 0.95. We’re aiming to calculate the power cost reduction and the payoff period for the capacitors. We’ll stick with the same numbers from before: a 5,000 kW load and 3,750,000 kWh of electricity consumption per month.
Calculating capacitor size to improve power factor to 0.95
At 0.65 
, 
, where 
= P.F. angle
At 0.95 
, 
Let’s calculate the apparent power based on a power factor of 0.65. We already know the real power is 5,000 kW.
= 7,692.30 kVA
= 7,692.30 kVA x 0.76 = 5,846.15 kVAR
We’ll now do the same calculation using the power factor of 0.95.
= 5,263.16 kVA
= 5,263.16 kVA x 0.31 = 1,631.58 kVAR
Take a look at the power triangle below. You can see how the added kVAR improves the power factor, and the kVA drops significantly.
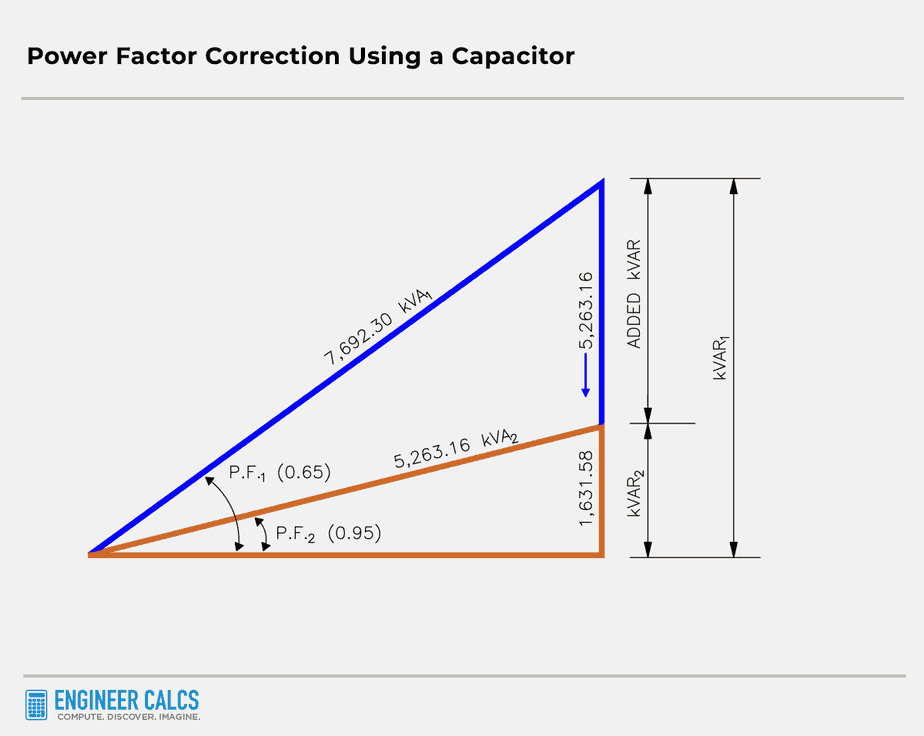
What size capacitor do we need?
= 5,263.16 kVAR – 1,631.58 kVAR = 3,631.58 kVAR
Capacitor cost
We’ll estimate the installation cost of a capacitor per kVAR to be $40.00.
That brings our total to $40.00 x 3,631.57 kVAR = $145,263.20
How much can we save on our monthly bill?
Here’s what we save by improving the power factor:
- Power factor penalty savings (from P.F. 0.65 to 0.85): $24,020.00
- Power factor credit (from P.F. 0.85 to 0.95): $12,010.00
Next, let’s calculate the loss reduction using the following formula:
(Monthly energy usage) x (Estimated 2% loss) x (Loss varies per ) x (kWh + Fuel cost adjustment) = 3,750,000 x 0.02 x 0.38 x ($0.35 + $0.006) = $10,146.00
Finally, let’s add up the total monthly savings:
Total savings per month: $24,020.00 + $12,010.00 + $10,146.00 = $46,176.00
Capacitor installation payoff
= $145,263.20 / $46,176.00 = 3.15 months.
It’s crystal clear that installing a capacitor in this situation is an absolute game-changer for Factory Z. Their profit margins will skyrocket in no time, and it’s a practical move that’ll make a huge difference.
Plus, the utility power factor penalty cost shows the impact on Utility X.
Conclusion
Utility power factor penalties can hit a company’s bottom line hard, especially with our heavy reliance on AC machines that need magnetism from their power source to work correctly.
Luckily, you can slash your electricity bill and keep your facility running smoothly by eliminating power factor surcharges with capacitors. This is especially important for businesses in states like California, where costs are always on the rise.
By using capacitors, you can increase your circuits’ load-carrying capacity and improve the voltage supplied to your equipment. It’s a win-win situation!
What do you think about utility power factor penalties? And how do you see the future of energy billing by utilities?
Featured Image Photo Credit: Stunteltje (image cropped)
SUBSCRIBE TO ENGINEER CALCS NEWSLETTER
its insulting. I have a small rental building. 8 people occupy approx. 3000 square ft. I have a penalty of 271.77 for my December bill. I don’t get it. I think I am being penalized for not using enough power? In any case its 50.00 per person.