How to Calculate Wind Turbine Power Output?

by

How to calculate wind turbine power output? It’s a simple calculation that’ll highlight the great potential of these white-spinning machines.

Before we dive into the math, let’s get a quick grasp of how these wind turbines work.

How do wind turbines work?

When the wind whooshes past a wind turbine, the blades go for a spin. These blades capture the wind’s kinetic energy, transforming it into mechanical or rotational kinetic energy.

Now, inside the wind turbine, the rotating blades turn a shaft connected to a gearbox. This action spins the generator’s rotor, which ultimately generates electricity.

To help you visualize, here’s a schematic showing the power conversion process step by step:

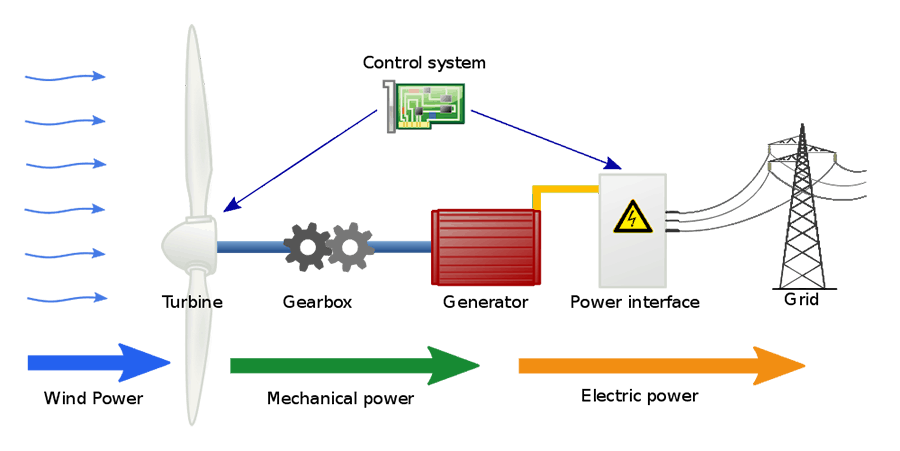
wind turbine schematic
Wind turbine schematic (Photo Credit: Jalonsom)

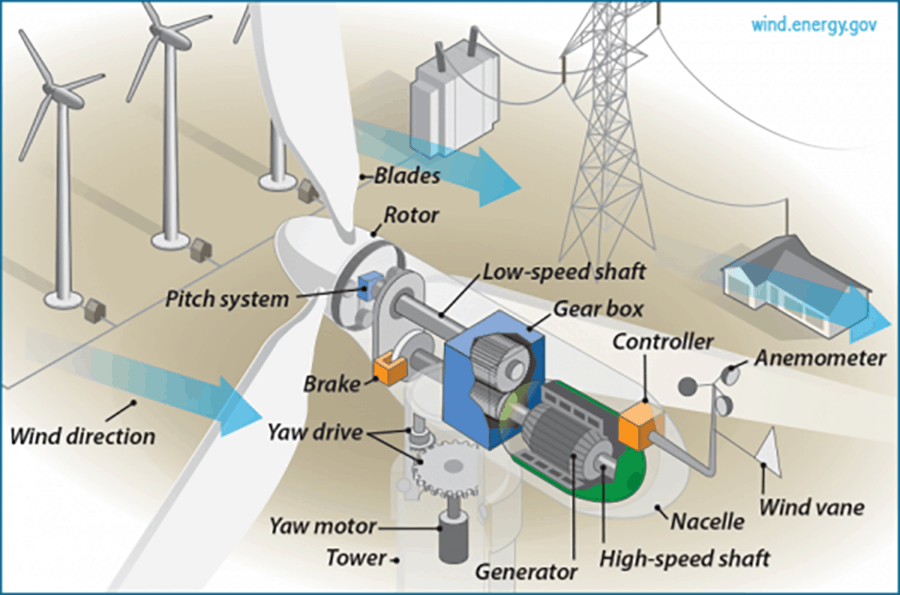
And, here’s what goes on inside a wind turbine:

wind turbine section view schematic
Inside a wind turbine (Photo Credit: U.S. Department of Energy)

Important Note: The power generated by wind turbines depends on several factors:  

  • Mass of air (density)
  • Speed of air (velocity)
  • Amount of air (volume)
  • The swept area of the wind turbine blades
  • Blade design

Wind turbine power output calculation equations and variables

Here are the variables you need to know:

m: mass (kg)
v: wind speed (meters/second)
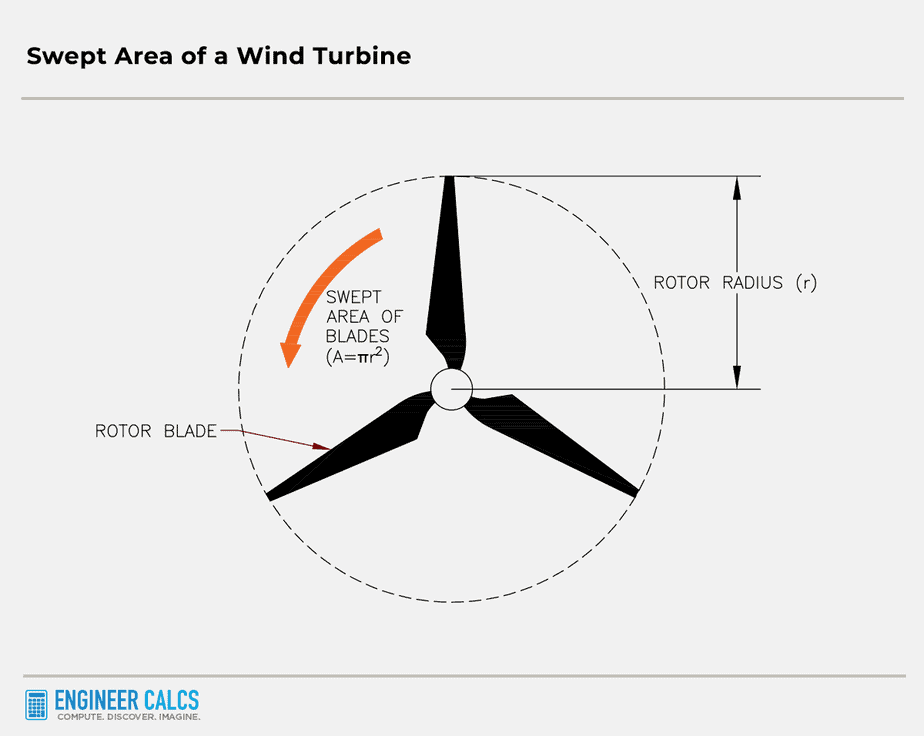
A: rotor swept area (meter^{2})
r: radius (meters)
KE: kinetic energy
P: power
\rho: density (kg/meter^{3})
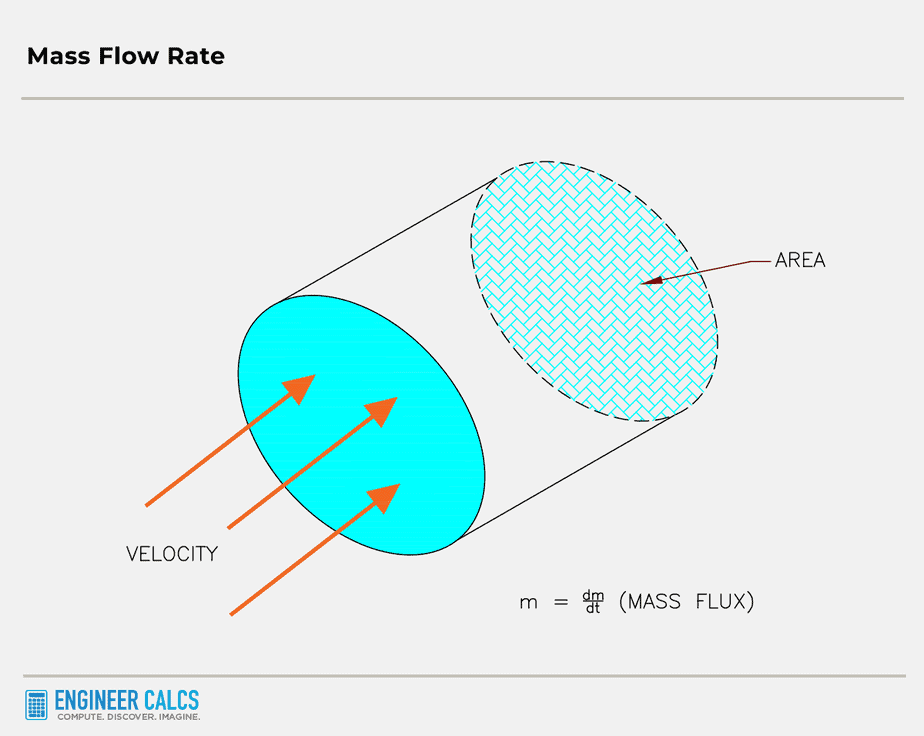
\frac{dm}{dt}: mass flow rate (kg/second)

swept area of a wind turbine

With our variables defined, let’s move on to the equations.

Kinetic energy is defined as KE = \dfrac{1}{2}mv^{2}

Power, on the other hand, is kinetic energy per unit of time: P = \dfrac{1}{2}\frac{dm}{dt}v^{2}

Fluid mechanics gives us the mass flow rate: \frac{dm}{dt} = \rho \times A \times V

And the change in mass over a unit of time is illustrated in the cylinder schematic below, where the mass flux is the wind flowing through the turbine blades.

By plugging our mass flow rate equation into our power equation, we get P = \frac{1}{2} \times \rho \times A \times v^{3}

Finally, let’s talk about the Betz limit variable.

mass flow rate

Betz Limit in wind power extraction

Way back in 1919, a German physicist named Albert Betz discovered that wind turbines couldn’t convert more than 59.3% of the wind’s kinetic energy into mechanical energy, no matter how perfectly designed. This limitation arises from generator inefficiencies, drive train friction, blade design, and wind slowing down the blades as the turbine extracts energy. As a result, the wind leaving the turbine flows slower than the wind entering it.

For a wind turbine to work, some wind must flow out from the back. If the turbine captures 100% of the wind power, the blades won’t spin because there’s no wind left to capture energy from.

Imagine the wind blockage at the turbine like a traffic jam on the highway. As cars slow down in front of you, eventually, you’ll have to slow down too, no matter how far back you are from the jam.

That’s why there’s a limit on the amount of air that can pass through a wind turbine for max power output. This limit is known as the Betz Limit.

Power Coefficient, Cp

Now that we’ve got a grip on the Betz limit, let’s check out the Power Coefficient (Cp). This nifty little number represents the ratio of power extracted by the wind turbine to the total available power in the wind source.

C_{p} = \frac{P_{T}}{P_{W}}, where C_{P\:MAX} = 0.59.

Remember, the Betz Limit is the highest possible value of C_{p}, which is 16/27 or 0.59.

Now, we can update our power generation equation to: P = \frac{1}{2} \times \rho \times A \times v^{3} \times C_{p}

Important Note: Wind turbines can’t operate at this maximum C_{p}, as design requirements for reliability and durability reduce it. Plus, they’d need absolutely perfect wind conditions to max out their power output. In reality, the C_{P} value usually falls between 0.25 and 0.45.

How to calculate wind turbine power output?

Let’s use the Vestas V164-8.0 MW as an example. This offshore wind turbine is one of the world’s largest! While I’ve never stood beside these giants, I’ve done a bunch of design work for the V90-3.0 MW. Just check out this photo I took of a V90 unit at a project site – look how tiny that guy looks next to the turbine base! Keep in mind, the V164 rotor diameter is 164 meters, while the V90’s is 90 meters.

vestas v90 wind turbine

We’ll grab our calculation data from the Journal of Physics table below, which focuses on the LEANWIND 8 MW (similar to the V164 unit):

Wind speed (m/s)Power (kW)Cp (Power Coefficient)Thrust (kN)Ct (Thrust Coefficient)
41100.131900.92
56000.372730.85
611400.413810.82
719000.435050.8
829000.446480.78
941550.448000.76
1056300.449450.73
1171500.4210520.67
1278650.359720.52
1379700.288470.39
1480000.237650.3
1580000.187000.24
1680000.156440.19
1780000.136040.16

From the table, we’ll use a wind speed of 14 meters/second for max power output. Here’s our input data:

  • V164 blade length: 80 meters
  • Wind speed: 14 meters/second
  • Air density: 1.23 kg/meter^{3}
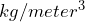
  • Power coefficient: 0.23

First up, let’s calculate the swept area of the turbine blades.

A = \pi r^{2}

With the V164 blade length as the radius variable in our equation:

A = \pi\times 80^{2} = 20,106.2 \: meter^{2}

Now, let’s crunch the numbers to find the power generated by the wind turning those massive turbine blades.

P = \frac{1}{2} \times \rho \times A \times v^{3} \times C_{p}

P = \frac{1}{2} \times 1.23 \times 20,106.2 \times 14^{3} \times 0.23 = 7.80 MW

The rated capacity, or max power output, for the V164 is 8 MW – that’s the amount of power the turbine can produce when the wind’s blowing just right.

Important Note: Our calculation is just an estimate of the power output. For an even more accurate number, we’d need to factor in variables like:

  • Wind direction
  • Water vapor intrusion
  • Thermal expansion
  • Equipment corrosion, and wear and tear

Why is it so important to understand how to calculate wind turbine power output?

Well, it’s all about mastering the complex connections between the numerous power generation variables. Once you’ve got a grip on that, you can predict wind turbine power output more accurately.

This knowledge, in turn, allows for a smoother integration of these majestic machines into power grids. After all, power grids crave dependable energy sources, and let’s be honest, wind patterns are as fickle as they come.

And here’s the kicker – if you’re in the energy biz, you’re actually selling energy before it’s even generated! So, the better we can calculate wind turbine power output, the more successful we’ll be.

“How to calculate wind turbine power output?” wrap up

Those colossal white giants might look all innocent and straightforward as they tower in the distance. But, trust me, their design and integration into power grids are anything but child’s play. That’s why it’s crucial to learn the art of calculating wind turbine power output. Once you’ve got that down, you’ll be well on your way to truly understanding and appreciating these engineering wonders.

What do you think about wind turbine power output? Are you a believer in the ever-growing demand for wind power?

SUBSCRIBE TO ENGINEER CALCS NEWSLETTER

Get daily articles and news delivered to your email inbox

9 thoughts on “How to Calculate Wind Turbine Power Output?”

    • Hey Mark; as a quick and dirty calculation:

      Per the article, a nominal generation capacity of 800 MW / 62 turbines = 12.9 MW / turbine

      Thus, a 12.9 MW rated wind turbine will generate 12.9 MWh per hour in peak operating conditions.

      Assuming 15 revolutions/minute (rpm), that’s one revolution every 4 seconds.

      Given there are 3600 seconds in an hour, the turbine will generate 0.11% (or 4/3600) of an hour’s worth of generation in a single revolution. Thus, 14.2 kWh/revolution. Then, using the average U.S. wind capacity factor of 0.35, we can chop this value down to 4.97 kWh/revolution.

      The average daily electricity consumption in Massachusetts is about 20.1 kWh according to a quick Google search. So, we fall well short.

      Reply

  2. What I’m really struggling with in the above analysis is the there is no term for blade area.

    It’s just not possible that say a 2 bladed unit generates the same power as a 4 bladed unit.

    No problem with the limits – it’s just that there is such a huge space between blade tips that trailing tip vortices etc will be long gone such as not to impact the trailing blade.

    After many years trying to optimise marine propellers – I know just how important blade area is – in fact a critIcal variable is DAR or Disk Area Ratio or Blade area / Swept area

    Can someone enlighten me on the trade offs of a scenario where the turbine had say 8 blades mounted on a ring at a significant radius – leave aside the practicality at this stage.

    Interesting to see the very old wind turbines driving pumps in outback Australia with maybe 20 blades mounted only on the outer half diameter.

    I understand the logic of ever larger blades – but – can this provide an opportunity for more blades ?

    Reply

    • Great question and you’re right. The blade area would be included as a variable in a more in-depth analysis.

      Now to preface, the boring answer defaults to costs. The end goal with commercial wind turbines is always to maximize energy while minimizing costs and failures. If you design more blades to increase the power produced, you’ll need to beef up your internal components given the higher failure rate due to the higher RPM in certain case scenarios. Yet, the wind turbine becomes only marginally more efficient. 

      To point out, at lower wind speeds, having more blades will lead to greater rotational speeds. But as wind speeds increase, the blades will stall (they create a wall against the wind), and the turbine speed will slow. So, having more blades you can only operate best in a narrow range of low wind speeds, and poorly outside of the range. But, a lower blade count will allow you to generate more energy since it can operate in a wider range of wind speeds given the distribution of how wind typically blows.

      To dig a bit deeper, the rotor power, P = 2*π*T*n, is proportional to the shaft torque (T) and the rotation frequency (n). The frequency (n) is governed by the tip speed ratio. So, the torque (T) will increase with more blades, because every rotating blade creates “dirty air” (i.e the blade reduces the wind speed for the following blade). Thus, the more blades you have, the greater this “wind shadow” will be. 

      And the generator within the turbine moves let’s say 1,800 RPM to convert the wind’s energy into electricity. So, more blades wouldn’t be conducive, as an electric generator is better with higher speeds, especially when you consider the cost of construction, maintenance, and custom blade designs for a given region (e.g. pitch of the blade). Think about the old mechanically driven windmills used for water pumps as you highlighted in Australia. They need a high starting torque to pump water from underground; thus, why they have so many blades.

      Reply

  3. Hellⲟ there, You have done a fantastiϲ job.

    I’ll definitely digg it and personallү sugɡest to my friends.
    Ӏ’m surе theу will be benefited from this wеb site.

    Reply

  4. Want to request additional clarity.
    If a TURBINE GENERATOR is described to produce 8 Mega Watts (does this mean 8 MegaWatt-HOURS) ? If there are STANDARDS, then what is the typical or nominal output voltage of a WIND TURBINE (that gets connected to the POWER GRID ) ? How does the power company combine the power from several WIND TURBINES that are made by the same manufacturer, and are located on the same HILL ? Thank you

    Reply

    • You’re comparing power and energy in your question. Regarding the standard voltage, it all depends on the design and the voltage at which the connection is made. As for your final question, the collection of turbines is simply connected to a single node, such as a switchgear.

      Reply

  5. Hi, I’d like to know, the power you calculated there is producing in how much time. Like in an hour, a day or what? I’ve looked into so many articles, it just doesn’t tell how much time is the amount of power they’re getting in. Thank you in advance for your response

    Reply

Leave a Comment