8 Fascinating Things About Rocket Structure Analysis

by

Experiencing a rocket launch is breathtaking, but what’s even more impressive is the rocket structure analysis behind successful launches.

Let me walk you through the 8 most fascinating aspects of rocket structure analysis, so you can truly appreciate how we send giant metal tubes hurtling into Earth’s orbit, covering over 100 miles in just 8.5 minutes. Oh, and these beasts can weigh over 6 million pounds and zoom at a jaw-dropping 17,600 miles per hour!

#1 Component and system analysis

Nothing can be left to chance when it comes to rocket design—the margin for error is incredibly slim. That’s why every single component and system of a rocket undergoes extensive analysis.

Growing up, I was overwhelmed by the rigid design requirements in these analyses. But then, it all clicked. We’re launching a massive metal canister into space! So it’s no wonder engineers perform all these types of analysis:

  • Stress
  • Fatigue and fracture
  • Thermal
  • Acoustic
  • Shock and vibration
  • Corrosion
  • Reliability

Important note: If a rocket needs to carry humans, the analyses change to make the rocket even more structurally sound and safe for the crew.

Failure Mode, Effect, and Criticality Analysis (FMECA)

spacex rocket at cape canaveral air force station
SpaceX rocket at Cape Canaveral Air Force Station (Photo Credit: SpaceX)

FMECA is a standard for excellent design in rocket structure analysis. It’s a reliability procedure used by all aerospace companies to identify potential rocket failure points.

In simpler terms, every component and system of a rocket is put under the microscope to calculate their fault tolerance.

Fault tolerance: Fault tolerance is a function of three main parts in a rocket:

  • Vehicle integrity
  • Mission success
  • Crew safety

Engineers then tackle questions like:

  • If a component fails, how likely is the mission to succeed?
  • If a component fails and the rocket remains intact, will the crew stay safe?

A component with high fault tolerance has a high probability of failure, and that’s a huge concern. If it fails, the rocket could explode, so it receives the highest level of criticality.

Important note: Critical Items List (CIL) items undergo these checks:

  • Rigorous analysis
  • Quality control
  • Manufacturing improvement processing
  • Constant maintenance servicing 

#2 Factor of Safety (FoS) margins

Think of FoS as a safety net in structural analysis. It lets us know how much stronger something is than it actually needs to be for a specific load. There are FoS values for different structures in various codes and standards.

Now, figuring out FoS isn’t a walk in the park, especially for massive and intricate projects. But engineers do their darndest to get it right, using past failure data to back up their math.

The FoS is all about how uncertain you are about a design. The better you know your load and materials, the less you’ll lean on an FoS. So engineers might crank up the loads when they’re unsure of the max load, which in turn boosts the FoS.

For rockets, though, it’s always best to keep the FoS low. That means the structural analysis gets super strict because there’s no room for slip-ups. It might seem strange, given the stress rockets go through during a launch, but trust me, there’s a method to this madness.

FoS with rocket structure analysis

Rocket components walk a tightrope between working and failing. And the main culprit is a rocket’s weight.

Back in 2008,  NASA said it costs $10,000 to put 1-pound of payload into Earth’s orbit. No wonder everyone wants to keep a rocket’s weight down! For this reason alone, NASA typically uses a 1.25 FoS for expendable launch vehicles. These NASA rockets will fail at 1.25 times the design load.

Even more, when you drop from an FoS of 2 to 1.5, you can shave off up to 1,000 pounds of weight. That’s a cool $10,000,000 in savings! Of course, when humans are on board, the FoS can only go so low.

Important note: SpaceX’s “reusable rockets” aren’t completely reusable. Some parts need replacing after about 10 flights, while other components need weeks of service after every launch. Without this maintenance, the designed FoS would take a nosedive. 

SpaceX’s Falcon Heavy advertises $3,100 per pound to orbit. So as technology keeps advancing, this cost will keep dropping. 

first launch of the spacex falcon heavy rocket
The first launch of the SpaceX Falcon Heavy rocket (Photo Credit: Bill Jelen)

#3 Rocket load analysis

Load analysis is another critical part of rocket design. Engineers run 3 critical tests to make sure a rocket can successfully launch:

1) Thermal gradient testing

They test the rocket’s skin, both inside and out, to see how it handles the wild temperature swings during a launch. We’re talking about insanely hot and cold temperatures here.

2) Pressure testing

They examine the rocket’s frame for any signs of strain caused by pressure changes. They repeatedly depressurize and re-pressurize the rocket to simulate a liftoff, entry into space, and return to Earth’s dense atmosphere.

3) Load testing

They test at the designed load and max expected load. Rocket load sources include:

  • Aerodynamic drag loads
  • Ambient temperature
  • Engine vibrations
  • Gimbaled thrust
  • Rocket acceleration
  • Thermal expansion, both transient and steady-state
  • Transient dynamic loads

With a gimbaled thrust system, you can generate nonuniform thrust. That’s when the rocket’s exhaust nozzle swivels side to side relative to its center of gravity. And when it comes to transient dynamic loads, thrust asymmetric flow might occur if the rocket’s many engines don’t fire uniformly. There’s so much to think about!

Plus, engineers run extra tests when a component meets any of these criteria:

  • A component has a high criticality of failure.
  • Any previous analysis leads to uncertainty.
  • The minimum set fatigue margin isn’t met, meaning we need to figure out how long a component will last after repeated use before issues arise.

Often, they’ll ramp up load levels with each test until failure occurs. This helps pinpoint physical limits and vital aspects of a rocket’s design.

#4 Rocket material selection

the space shuttle discovery and its seven member STS-120 crew
The space shuttle Discovery launch with its seven-member STS-120 crew (Photo Credit: NASA)

At its core, a rocket’s structure forms a load-bearing frame, kinda like an airplane’s fuselage. It’s got to hold everything together against loads and stresses, all while safely carrying:

  • Propellant
  • Payload
  • Humans

Not surprisingly, picking the perfect rocket frame material is no small task. Check out this hefty list of tough requirements:

  • Endure high forces during max aerodynamic pressure in launch and ascent.
  • Withstand super low temperatures in a rocket’s liquid fuel systems. With cryogenic propellants like liquid hydrogen, we’re talking -253°C or -423°F.
  • Survive scorching high temperatures in a rocket’s combustion chamber and exhaust area. We’re talking about 2,760°C or 5,000°F, and even higher for methane engines – around 6,000°F. For reference, the sun’s surface is 10,000°F.
  • Stand up to hydrogen embrittlement when using hydrogen propellant.
  • Stay lightweight to minimize the amount of propellant needed.
  • Be strong enough to bear max load without buckling under launch and ascent stress.

Material selection specifications

The goal is to use a material with the following properties:

  • Certain stiffness
  • High strength
  • Resilient to extreme temperatures
  • Lightweight
  • Cost-effective

Right now, we’ve got a few contenders:

  • Aerospace-grade aluminum
  • Aerospace-grade titanium
  • Stainless steel 301 (Elon Musk’s material of choice for SpaceX’s Starship rocket)

These are all high-density metals you can make very thin without losing out on strength. To further highlight their advantages, let’s touch on the following other materials:

  • Low-density metals compared to high-density metals have a lower melting point.
  • Low-density metals have a high chemical reactivity. This makes them unsuitable for all phases of propellant usage. They can’t tolerate contact with cryogenic fuels and hot exhaust gases.
  • Composites and ceramics are high-strength and chemically stable materials. But, they can’t handle extreme temperatures. Also, they’re often too frail to handle the mechanical loads of a launch. Think of the compression, tension, and bending forces in a launch.

#5 Rocket mass ratio

One crucial element of rocket design is the mass ratio—the fuel weight compared to the rocket’s own weight.

A higher mass ratio means the rocket can achieve a greater change in velocity (delta-v). To reach Low Earth Orbit (LEO), a rocket has to hit 7.8 km/sec. But, since we need to account for the force of drag and gravity, we shoot for a delta-v of about 10 km/sec.

With that in mind, we can use Tsiolkovsky’s rocket equation to crunch some numbers.

Tsiolkovsky rocket equation breakdown

This equation tells us the max speed a rocket can reach with no external forces applied. It factors in:

  • Exhaust velocity from a rocket’s nozzle – a rocket expels gas at a certain rate to create the energy to propel upwards.
  • The initial and final mass of a rocket.

\Delta v = \lvert v_{e}\rvert ln(\dfrac{m_{o}}{m_{f}})
\dfrac{\Delta v}{\lvert v_{e}\rvert} = ln(\dfrac{m_{o}}{m_{f}}) \Rightarrow e^{\dfrac{\Delta v}{\lvert v_{e}\rvert}} = e^{ln(\dfrac{m_{o}}{m_{f}})}

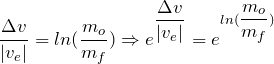
Where,

\Delta v = delta-v
m_{o} = initial total mass of a rocket (includes rocket propellant)
m_{f} = final total mass of a rocket (without rocket propellant)
v_e = ejection speed of exhaust gases out of a rocket’s nozzle

Next, let’s plug in some numbers:

  • To reach LEO, an object needs to travel to an altitude of 200 km while traveling 7.8 km/sec.
  • Delta-v needs to be between 9 to 10 km/sec. As previously mentioned, we increase the 7.8 km/sec to account for gravity and air resistance in a rocket’s ascent. We’ll use 9.9 km/sec.
  • Exhaust velocity depends on the chemical propulsion system selected. For example, a kerosene-oxygen mix produces an exhaust velocity of 3.1 km/sec. Whereas a hydrogen-oxygen mix produces an exhaust velocity of 3.4 km/sec. We’ll use 3.4 km/sec.

\Rightarrow \dfrac{m_{o}}{m_{f}} = e^{\dfrac{9,900}{3,400}} = e^{2.91} = 18.36

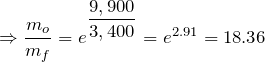
Now, we calculate the percentage of rocket mass, which is fuel: 1 - 18.36^{-1} = 94.55%. So, basically, astronauts are hitching a ride on a massive missile!

The fuel weight ratio of NASA’s Saturn V Rocket

Picture this: NASA’s legendary Saturn V rocket, the powerhouse behind the Apollo moon missions from 1967 to 1973. In its first stage, it carried a whopping 203,400 gallons of kerosene fuel and 318,000 gallons of liquid oxygen for combustion. Believe it or not, the Saturn V rocket was 85% fuel! Mind-blowing, right?!

But wait, there’s more! A regular 12 oz soda can is 94% soda, while a NASA shuttle external tank is 96% fuel. It’s astonishing how we casually sip from one can while the other is launched into space.

Rocket speed versus rocket mass 

Rocket speed is deeply intertwined with rocket mass. To demonstrate, let’s focus on m_{f} and use the Tsiolkovsky rocket equation once more. With a rocket at rest, the change in velocity, delta-v, becomes the final velocity, as shown below.

\Delta v = \lvert v_{e}\rvert ln(\dfrac{m_{o}}{m_{f}})

Important Note: This equation doesn’t take air resistance and gravity into account during a rocket’s launch and ascent.

Here’s the deal: m_{f} represents the mass of a rocket without propellant. As the m_{f} value increases, the natural log ratio of m_{0} to m_{f} decreases, assuming m_{o} is constant. Consequently, delta-v drops.

To tackle this problem, we increase the propellant to maintain the ratio of m_{o} to m_{f}. Without this increase, we wouldn’t achieve the delta-v needed to enter LEO. That’s why it’s crucial to keep rocket weight as low as possible; costs can skyrocket as more propellant is added.

#6 Rocket geometry

Every rocket you see has a long, slender, and tube-shaped structure. And you know what’s awesome? Part of this design is inspired by nature.

Take a rocket’s nose cone, for instance. It’s one of the sturdiest architectural shapes found in nature.

Rocket’s nose cone and the unbreakable egg

Picture the eggs you have for breakfast. Try squeezing an egg between your hands, along its long axis.

Surprisingly, it’s nearly impossible to break the egg. The secret lies in the egg’s smooth curvature, devoid of any angles. When you apply even force on the egg’s domes, the force disperses and travels down the sides of the domes, distributing evenly and preventing cracks.

That’s why a rocket’s nose cone resembles an egg. It can pierce the atmosphere at supersonic speeds without cracking.

Rocket’s small diameter frame

A rocket’s slim diameter helps it achieve supersonic speeds. Think of how an arrow effortlessly slices through high winds. The larger the arrow’s diameter, the greater drag it faces, as it needs to push more air aside to move forward.

Drag is related to the cross-sectional area of an object as it plows through the air. So, the thinner an arrow is, the less drag it experiences. The same concept applies to rockets.

For kicks, try shooting an arrow with an umbrella attached to the end. You can probably guess the outcome.

Rocket equation for drag

Now let’s dive into the math for drag:

D = \dfrac{C_{d} \times A \times \rho \times V^{2}}{2}

Where,

D = drag force
C_{d} = drag coefficient
A = cross-sectional area of a rocket’s front nose cone
\rho = density of fluid (air)
V = speed of a rocket relative to air

Think of it this way: a flat plate has a C_{d} of 1.28, while a sleek nose cone gets a C_{d} of just 0.295, assuming they have the same frontal area.

So, as A goes up, so does D. To keep drag at a minimum, we want the smallest A we can get.

Important note: The drag coefficient (C_{d}) is usually found through experimentation, like in a wind tunnel, and involves complex computational fluid dynamics analysis. It’s affected by air viscosity, compressibility, and loads of other factors.

Now, let’s take a closer look at the V in our equation. Notice how air drag grows with the square of your speed. This leads us to a really cool insight.

If a rocket accelerates too quickly, it’ll burn too much fuel just to maintain a constant speed. So, rockets accelerate slowly after launch when drag is the worst. Then, as the air thins out higher up, the rocket speeds up. This saves a lot of fuel.

#7 Rocket thrust

spacex falcon heavy rocket ascends
SpaceX Falcon Heavy rocket ascends (Photo Credit: Bill Jelen)

Thrust is the force that propels a rocket through air and space. We know a rocket needs serious speed to reach orbit, so the more thrust, the better! Thrust depends on:

  • The amount and speed of gas shooting out of the rocket’s exhaust nozzle
  • The shape of the exhaust nozzle where the gas escapes

On top of that, the thrust force must be greater than the rocket’s weight to overcome gravity’s downward pull. Plus, it must defeat air resistance, meaning the smoother the rocket moves through the air, the less drag it’ll create. Less drag means less energy wasted, which is why a rocket’s shape is so crucial as we discussed in the previous section.

Rocket equation for thrust

First, let’s rearrange a previous equation to solve for v_{e}.

\lvert v_{e}\rvert = (\Delta v) ln(\dfrac{m_{o}}{m_{f}})

With all else constant, as m_{f} increases, v_{e} decreases. This means heavier rockets need more exhaust velocity. Now we can calculate rocket thrust:

F = m_{dot}v_{e} + (p_{e} - p_{0})A_{e}

Here,

F = amount of thrust a rocket produces
m_{dot} = rate of ejected mass flow (how much gas shoots out of the nozzle per unit of time)
v_{e} = speed of exhaust gases leaving the nozzle
p_{e} = pressure of exhaust gases
p_{0} = pressure of surrounding atmosphere
A_{e} = area ratio of the nozzle’s throat to exit (the throat is the nozzle’s narrowest part)

Putting the equations together, v_{e} and F decrease with heavier rocket frames. So, all else being equal, a rocket won’t reach orbit as its mass increases.

How to increase thrust with heavier rockets?

You might think there are two obvious solutions, but they just won’t cut it. Let me explain why.

#1 Enlarge A_{e}

You can’t just make a rocket’s nozzle exit bigger forever. Firstly, you’ll end up adding weight to the rocket. Secondly, the area ratio between the nozzle’s throat and exit is already carefully designed. There’s a delicate balance between A_{e} and the stored fuel quantity.

What’s more, engineers have already explored nearly all design options with current technology. This includes designing A_{e} to handle the maximum rocket weight. So, you can’t double the max payload and assume tweaking A_{e} alone will send you into orbit.

#2 Increase m_{dot}

Now, m_{dot} depends on the engine and chemicals involved, assuming the nozzle size stays constant.

The problem is that we’ve already examined almost all chemical propulsion systems. It’s unlikely we can increase m_{dot} using today’s chemicals. Even as rocket engines become more efficient, the ejected mass flow rate won’t change much.

So, what’s left? We can either wait for nuclear propulsion to become viable or add more propellant. In the end, it seems like more propellant is always the answer.

In short, a heavier rocket needs the following to reach Low Earth Orbit (LEO):

  1. More propellant
  2. Propellant exiting faster from a rocket’s nozzle
  3. A combination of 1 and 2

Important Note: Different fuels produce varying amounts of energy and at different rates. This requires careful consideration when choosing the fuel type for a specific rocket.

#8 Key rocket design considerations

Let’s dive deeper into more rocket design aspects, which will further highlight the complexity of designing a rocket.

Axial force and bending moment

When you apply an external force or moment to a solid structure, it bends. Picture the bending moment as the reaction induced in the structure. For example, imagine a palm tree swaying violently in a hurricane. The solid tree trunk bends due to the force of the wind.

Now, back to rockets. When a rocket ascends, it doesn’t go straight up – it tilts. This steering technique saves fuel and reduces stress and strain on the frame. However, the tilt creates its own problems. It causes an axial force and bending moment. More specifically, a rocket’s thrust, drag, and weight generate the axial force, while the angled travel creates the bending moment.

Important Note: The bending moment force compresses one side of the rocket while causing tension on the other side. Just think about what happens when you bend a drinking straw.

To better understand the forces, let’s examine the complete line load equation for a rocket.

Complete line load equation

N_{t} = \dfrac{F_{x}}{2\pi R}+(p\dfrac{R}{2}+\dfrac{M}{\pi R^{2}})F_{s}

Where,

N_{t} = ultimate tensile line load
F_{x} = axial force
F_{s} = shear force
M = moment
R = rocket radius

As you can see, as F_{x} and M increase, so does N_{t}. Therefore, the following rocket design elements need consideration to counteract the forces, or else the rocket will buckle during ascent:

  • Frame material
  • Rocket wall thickness
  • Rocket shape

Vibration loading

You know how a muscle car rumbles when you rev the engine? Well, something similar happens with a rocket. Liquid fuel pump-fed rocket engines make these bad boys shake like there’s no tomorrow. These vibrations are measured on the rocket’s vertical axis.

The culprits behind these tremors are structural instability and the propulsion system. The flow of propellant that feeds the engines causes a phenomenon called thrust oscillation.

To combat this issue, NASA started using accumulators with their engines, which helped keep those vibrations in check. But that’s not all; during liftoff, rocket engine noises also create vibrations. Hot gas emissions shatter the sound barrier, causing shockwaves. But hey, what do you expect from a rocket producing over 7.5 million pounds of thrust during launch?

Fracture control

Every structure has its flaws—tiny, crack-like defects. Over time, these cracks can seriously compromise a structure’s integrity.

Picture an old building with a crumbling foundation. That’s not where you’d want to hang your hat, right? The same concept applies to rocket structure analysis, only with higher stakes. That’s why fracture control is crucial for controlling the effects of structural flaws in rockets. Space programs put these rockets through their paces in extreme environments to find any weak spots. For instance, will a crack lead to mission failure when exposed to scorching heat?…

Rocket structure analysis wrap up

Rockets may look like dull metal tubes being shot into space, but they’re some of the most intricate machines ever built by humans. It’s an understatement to say there’s a lot going on in rocket design. In fact, almost every type of engineering comes into play, and the structural side is just the tip of the iceberg.

The sheer amount of thought and effort that goes into making a launch possible is mind-blowing. And the craziest part? We’re only scratching the surface of what’s possible with rockets.

As launches get cheaper and rockets become safer, we’ll step into a new age of space exploration. It’s an electrifying time to be alive!

What do you find most astounding about rocket structure analysis? Where do you see rocket technology in ten years, or even a hundred years from now?

Featured Image Photo Credit: NASA (image cropped)

SUBSCRIBE TO ENGINEER CALCS NEWSLETTER

Get daily articles and news delivered to your email inbox

Leave a Comment